本篇文章内容由[中国幕墙网ALwindoor.com]编辑部整理发布:
摘要:拉索幕墙是风敏感结构。特别是单层索网和单拉索支承结构刚度小,自振频率低,对风荷载十分敏感。形状较简单的中小跨度索结构,结构的风动力效应可采用平均风荷载(词条“荷载”由行业大百科提供)乘以风振系数的方法近似考虑。跨度大于25m的平面索网结构或跨度大于60m的索桁架结构需要通过风振响应分析确定风动力效应。本文对某工程项目中的单层索网进行风振响应分析,利用SAP2000建立有限元模型,将模拟出的风荷载施加到拉索的各个节点上,进行风振响应分析

关键词:单层索网、风振响应分析、风振系数、时域分析法
引言
单层索网玻璃幕墙具有简洁、通透的特点,广泛运用于大堂,展馆和机场等建筑工程中,满足建筑师对通透性的要求。单层索网具有刚度小、重量轻、自振频率低等特点,因此索网结构对风荷载的作用非常敏感,易产生风振响应。因此在JGJ257-2012 《索结构技术规程》中规定:跨度大于25m的平面索网结构或跨度大于60m的索桁架结构;索结构的基本自振周期大于1.0s;体型复杂且较为重要的结构,这三类应通过风振响应分析确定风动力效应。
结构风振响应分析方法主要有频域分析法和时域分析法。其中频域法就是利用傅里叶变换将风荷载变换为一系列的简谐荷载,最后再将结构在每个简谐荷载下的响应叠加起来得到结构的总响应。这种方法的缺点是不能考虑结构的非线性,计算结果不够精确。时域分析法则是直接运用风洞试验(词条“风洞试验”由行业大百科提供)的风压(词条“风压”由行业大百科提供)时程或数值模拟的风压时程作用于计算模型上,通过在时间域内直接求解运动方程得到结构的响应,能够考虑到结构的非线性影响,对于索网结构这种非线性柔性结构具有一定的优越性。本文通过四方城的拉索幕墙工程实例,采用时程分析法,运用数值模拟获得风速时程,利用有限元软件SAP2000建模,将模拟出的风荷载施加到拉索的各个节点上,进行风振响应分析。
1.工程概况
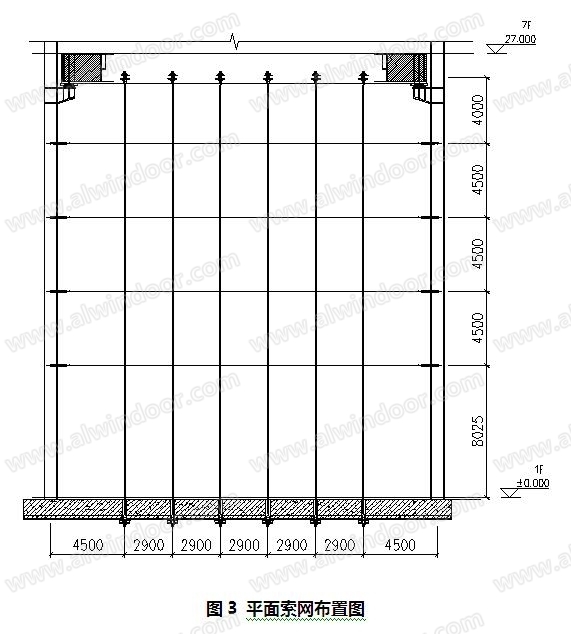
某工程位于上海市浦东新区前滩板块,钱家滩路以南、耀龙路以西、海阳路以北、江泳路以东,地上部分建筑物的使用功能为商业、办公,最大建筑幕墙标高为49.8m,建筑效果图如图1所示。拉索幕墙位于两栋塔楼之间,为单层索网结构,如图2所示。竖索直径60mm,预拉力500kN,跨度27m,间距2900mm,顶部连接到主体大钢梁上,底部连接到首层混凝土梁;横索直径20mm,预拉力20kN,跨度23.5m,间距4500mm,两端连接到两栋塔楼的楼层梁上,图3为平面索网布置图。主体结构的刚度足够大,忽略拉索支座位置主体结构的变形,所以计算时未考虑主体结构变形对索网的影响,假定索网四周的支座都是固定(词条“固定”由行业大百科提供)铰支座。


2.单层索网风振响应分析
2.1 时程分析法
时程分析法的主要步骤为:1)通过风洞试验或数值模拟来确定风荷载时程;2)确定结构的质量M,阻尼C,刚度K等参数,建立有限元模型;3)将风荷载时程作为外荷载时程作用到有限元模型上;4)采用瞬态分析方法得出结构的动力响应,从而得到风振系数。
2.2 风荷载的模拟
当没有风洞试验数据时,可利用数值模拟来获得风荷载时程。风荷载本质上是一种随时间波动的动力荷载,常把风荷载分为平均风和脉动风。平均风是在给定时间间隔内不随时间而改变的量。脉动风具有随机性,随时间和空间变化。脉动风速可通过其功率谱来描述。常见的风速谱有:不考虑湍流积分尺度随高度变化的Davenport谱、Harris谱等;考虑湍流积分尺度随高度变化的VonKarman谱、Simiu谱等。
结构风振响应分析中的风速时程可以通过数值模拟方法得到。相关节点的风速时程曲线通常用自回归法(AR法)、谐波叠加法、逆傅里叶变换法和小波分析法等方法来模拟。AR法是一种高效的模拟具有时间相关性和空间相关性的相关节点风速时程方法,具有模拟精确、计算速度快、计算稳定等特点,广泛地应用于实际工程中。本文采用由陈学伟等公开的风时程生成程序[7],输入相关参数生成脉动风速时程。该小程序就是采用自回归模型AR模拟脉动风速时程,其中风速谱采用DavenPort谱。上海地区50年一遇基本风压0.55kN/m2,C类地面粗糙度,地貌指数α=0.22,拉索幕墙位于两栋塔楼之间,局部体型系数取1.2。
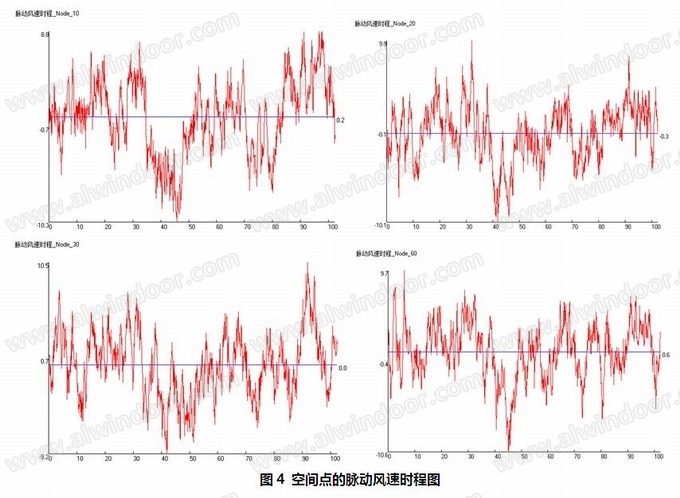
通过AR法计算可得到空间点的模拟总风速时程,然后乘以空间点的受风面积和受风面体型系数,可以得到风压时程。风时程生成程序将生成SAP2000的时程动力分析代码,导入SAP2000中进一步进行风振时程分析,图4显示了多个节点的脉动风速时程图。
由文献[7]可知,模拟风速谱与目标谱基本吻合,如图5所示,虽然在低频率有所偏离,但是在结构自振频率附近相当吻合,这表明采用AR法模拟的脉动风速时程是合理有效的。

2.3 风振系数计算
风振系数包括荷载风振系数和位移风振系数。关于单层平面索网结构风振响应的非线性特研究已表明[13],索网在第一阶模态在所有模态中占较大比重。因此可以采用基于响应的位移风振系数。结构在风荷载作用下的峰值响应Umax与平均风作用下的静位移Us之比就是位移风振系数。风荷载作用下的峰值响应Umax等于脉动风荷载作用下的峰值位移响应Ud与平均风作用下的位移Us之和。
位移风振系数为:β=Umax/Us=(Ud+Us)/Us=1+Ud/Us,式中:Ud为脉动风荷载作用下的峰值位移响应,Us为平均风作用下的位移。
我国荷载规范采用的是荷载风振系数,总的风荷载作用与平均风力之比就是荷载风振系数,其表达式为β=(Fd+Fs)/Fs=1+Fd/Fs,式中:Fd为第1阶风振惯性力峰值,Fs为平均风力。参考建筑结构荷载规范[14],Fs=w0μsμzA,Fd=g(2πf)2mσq,其中A为荷载作用面积;g为峰值因子,取2.5;f为第1阶自振频率;m为对应的质量;σq为第1阶位移均方根。
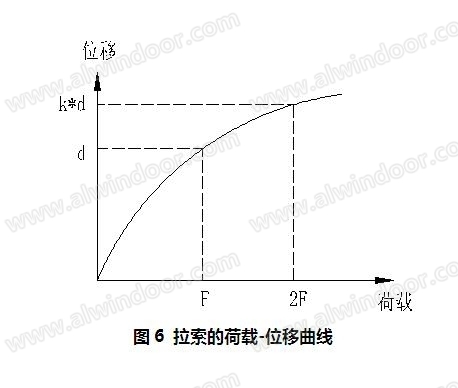
拉索的非线性表现为变形越大其刚度越大,所以荷载和变形不是线性关系。拉索的荷载-位移曲线如图6所示,设荷载F作用下的位移为d,则2F作用下的位移k*d,其中k<2。所以在计算位移风振系数时如果用总位移响应除以平均风作用下的静位移,得到的值是小于实际风振系数的,应该是按1+Ud/Us计算。
采用有限元软件SAP2000建立计算模型,拉索选用索单元,竖索直径60mm,预拉力500kN,横索直径20mm,预拉力20kN,不考虑主体结构的变形,索网四周的支座均为固定铰支座。荷载加在到各个节点上。脉动风荷载和平均风荷载分别加载。脉动风荷载由上述数值模拟所得的风压时程进行加载。平均风根据荷载规范不考虑风振系数计算得到:基本风压0.55kN/m2,C类地面粗糙度,30m标高处的风压高度变化系数取0.88,风荷载局部体系系数取1.2,连乘得到平均风荷载为0.58 kN/m2,再乘以每个节点的受荷面积得到集中力,把集中力加载到计算模型中进行计算。
平面索网节点较多,提取侧边和中间两个拉索上的几个典型节点进行分析,所提取节点分布如图7所示。表1列出各典型节点的位移风振系数,荷载风振系数及按荷载规范计算的阵风系数。

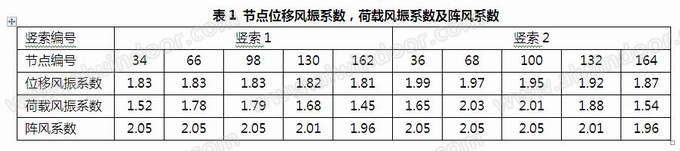
由上述计算数据可知,边部拉索的风振系数较小,拉索跨中的风振系数最大,其原因是横索对边部的拉索帮助更大,其刚度较大,对应的风振效应就较小。荷载风振系数各个点的变化较大,位移风振系数相对稳定,位移风振系数和荷载风振系数的均方根基本一致,工程中可以用位移风振系数计算风荷载。以下分析仅考虑位移风振系数。
2.4 进一步分析计算
以上分析仅考虑了竖向拉索的预拉力为500kN的情况,当竖索的预拉力分别为300kN,100kN的风振系数详见表2。由计算结果可知,随着预拉力的减小,索网刚度变弱,其风振系数逐渐变大。
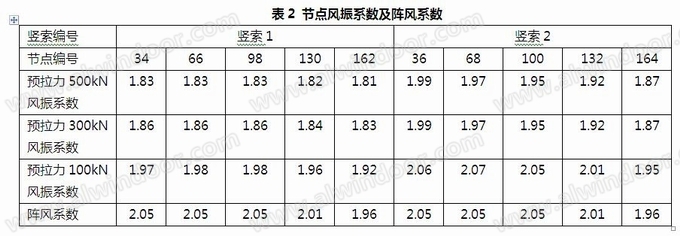
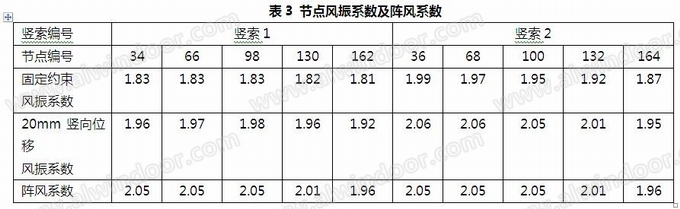
以上分析没有考虑主体结构的变形对索网的影响。进一步分析,考虑顶部钢梁在风荷载作用下竖向变形有20mm,则在计算模型的竖索顶部施加20mm的竖向位移荷载,重新计算得到各个节点的风振系数见表3。此工况下索网的第一自振周期T=3.22s,而预拉力100kN时索网的第一自振周期T=3.25s,两种工况的自振周期相近,通过表2和表3的相应数据比较可知其风振系数也基本一致。
横索直径改为60mm,预拉力500kN,竖索还是直接60mm,预拉力500kN,计算风振系数如表4所示。由计算结果可知,横索加大直径和预应力(词条“预应力”由行业大百科提供),使得整个索网的刚度有所提高,风振系数比原来横索直径为20mm时的数值较小。

表5对以上计算结果进一步汇总比较可知,索网的第一自振周期越小,风振系数也对应减小。本工程索网的跨度为27m,与索结构技术规程[1]规定的25m相差不大,当不考虑主体位移时,自振周期为1.5s,风振系数可取1.9;当考虑主体竖向位移20mm,索网自振周期3.2s,风振系数应取2.0。

3.结语
单层索网属于柔性结构,对风荷载敏感。通过对某工程平面单层索网的风振响应分析,分别计算比较了索网在不同预拉力及边界条件下的风振系数,可以得出以下结论:
1) 荷载风振系数在索网上下左右边部区域的数值较小,在中间区域最大,和文献[3]推导出的结论基本一致。位移风振系数相对稳定,也表现为边部较小,中部最大。荷载风振系数的均方根和位移风振系数基本一致,所以在工程中可以用位移风振系数来计算风荷载。
2) 拉索的预拉力对索网的刚度影响大,预拉力越大索网刚度越大,其风振系数取值可以减小。
3) 考虑主体结构的变形对索网的影响,拉索的预应力有损失,导致索网的整体刚度变弱,根据计算结果比较,得到的风振系数会增大。
4) 本工程索网跨度27m,与索结构规程规定的25m相差不大,当不考虑主体位移时,自振周期1.5s,风振系数可取1.9;当考虑主体竖向位移20mm,索网自振周期3.2s,风振系数应取2.0。
5) 由于单索结构体系对支承边界条件比较敏感,为了准确获取风振系数,建议进行索网计算时将支承边界结构和索网结构合成一体分析。
参考文献
[1]《索结构技术规程》JGJ257-2012 中国建筑工业出版社
[2] 蔡建国,冯健,曹华兵,等.单层索网玻璃幕墙的风振响应分析[J].沈阳工业大学学报,2010,32(3):355-360.
[3] 姚金满,段洪涛.玻璃幕墙单层索网结构的风振与实用设计[J]. 建筑结构, 2012,42(1):677-681.
[4] 王莺歌,李正农.索桁式玻璃幕墙风荷载时程模拟及风振响应[J]. 昆明理工大学学报(自然科学版), 2011,36(2):26-31.
[5] 季俊杰,陈红宇,苏骏,等.预应力单层索网幕墙结构的风致响应计算[J].建筑钢结构进展.2011,13(3):37-41.
[6] 武岳,冯若强,沈世钊.单层平面索网幕墙结构的风振响应分析及实用抗风设计方法 [J].计算力学学报,2007,24(5):633-637.
[7] 陈学伟,韩小雷,郑宜,等.高层建筑结构风振时程分析软件的技术研究[J].华中科技大学学报(城市科学版).2008,23(3):136-139.
[8] 张文元,郑朝荣,张耀春,等. 某景观烟囱顺风向风振响应分析与风振系数确定[J].建筑结构.2010,40(2):97-99.
[9] 汪楚清,孙清,王虎长,等. 拉线塔风振系数取值研究[J].钢结构.2016,5(31): 31-36.
[10] 杨霄,葛家琪. 荷载风振系数和位移风振系数关系的初步研究与设计建议[J].工业建筑.2008: 1815-1821.
[11] 魏德敏,李杰超.大跨索网结构风振系数分析[J].华中科技大学学报(城市科学版).2008,25(3):17-19.
[12] 张建胜,武岳,沈世钊.单层网壳结构的风振响应与抗风设计[J].武汉理工大学学报.2006,28(7):63-66.
[13]吴丽丽,王元清,石永久.单层平面索网结构风振响应的几何非线性特性研究[J].振动与冲击,2007,26(4):30-34.
[14]《建筑结构荷载规范》GB 50009-2012 中国建筑工业出版社

