本篇文章内容由[中国幕墙网ALwindoor.com]编辑部整理发布:
1 前言
我们在幕墙设计实践过程中,常常会遇到既有建筑改造之前,需要检测以判断幕墙产品的可靠度;幕墙结构工程师和幕墙系统设计师对同一个节点(词条“节点”由行业大百科提供)细部安全的可靠性(词条“可靠性”由行业大百科提供)理解大相径庭;幕墙结构评审时,专家的评判和被审查者的工程实践经验和理论认知差距较大时,评审往往陷入尴尬的局面……。实际上新材料、新工艺、新技术在幕墙工程应用中遇到的审查;复杂空间结构设计带来的跨专业问题;建筑幕墙使用寿命到期问题;由于建筑功能要求日益苛刻的需要,导致幕墙系统结构设计的复杂性;灾害性气候对幕墙的损害,而导致社会公共安全及索赔问题,都对建筑幕墙可靠性提出新的要求和挑战。
一种适合于幕墙的结构可靠性理论,可用来指导技术人员进行科学合理的设计,除去思想上的疑惑,在结构安全设计上提高效率,在安全评估上能有明确和快速决断的依据,有效降低幕墙维修的成本;同时,随着我国幕墙工程越来越复杂,幕墙系统结构安全的可靠性日益引起行业重视,它关系到幕墙工程的质量安全和社会成本总投入,也涉及到幕墙技术的发展和理论创新。
2 可靠性概念
幕墙作为一个产品,系统可靠性是靠前期设计、生产制造、施工安装、使用管理等一系列工程环节来保障的,但首先是被设计出来的。传统的结构设计和强度校核是基于确定性分析,即结构计算时假定结构的几何尺寸、材料的物理性能以及所受的载荷均是确定的。但实际上这些因素都带有随机性:例如建筑立面上的风等载荷都是不确定的,钢铝(词条“铝”由行业大百科提供)结构材料中用的材料物理性能参数可能与提供的有所差别,名义尺寸与实际结构不完全一致;计算中引入的假设和计算模型与实际情况有偏离等等。这些因素都会影响对结构真实可靠性评价。惯用的确定性分析中为了考虑这些不确定因素的影响只是简单地引入安全因子概念,使许用应力略低于材料地试验数据或认为地加大几何尺寸,以抵消一些偏危险地因素,提高安全感。安全因子K:

尽管如此,结构发生破坏的事件还时有发生。这是由于客观世界的规律引起:(1)随机现象,是因为难以全部估计的多种偶然因素存在,通常无法事先准确断定未来事件的结果,表现出因果关系不充分,在一些条件下,某些结果并不总是满足“必然如此”。它除了客观事物有这种特性外,还包括主观认识的不完整性。(2)模糊现象,是因为难以对周围某些事物给出明确的定义和确定性的评定标准,通常无法绝对判定事物属于何类型。判断事件属性时其边界的不清楚性是模糊事件的特点。以强度问题为例,如计算求得的最大应力值小于或等于许用应力值,则认为结构没有破坏,但计算值超过哪怕是超过一点点,则结构被认为是失效了。而事实上应力的允许范围具有模糊性,从允许到不允许是逐步过渡的。(3)不准确或不完整的信息:对自然界现象认识不足或辨别和了解能力的局限性。
在工程实践中,上面三种不确定现象均存在。二十世纪五十年代以来,学者和专家对可靠性进行了不断研究后,形成了基于上述规律的较为成熟的可靠性理论--随机可靠性分析理论。
根据GB/T21086建筑幕墙[1]的定义是:由面板与支承结构体系(支承装置(词条“支承装置”由行业大百科提供)与支承结构)组成的、可相对主体有一定位移能力或自身有一定变形能力、不承担主体结构所受作用的建筑外围护墙。幕墙是一个结构概念也有别于传统的建筑结构体系,由于它由面板和支撑结构体系组成,兼顾工程结构、机械设计范畴。可靠性概念可从这两方面来进行考虑。
2.1 建筑结构可靠性
[2]建筑结构可靠性包含了结构安全性、适用性、耐久性几个方面的含义,即(1)能承受在正常施工和正常使用时可能出现的各种作用;(2)在正常使用时具有良好的工作性能;(3)在正常维护状态下具有足够的耐久性能;(4)在偶然事件发生时及发生后,仍能保持必须的整体稳定性。
在规定的时间和条件下,工程结构完成预定功能的概率,是工程结构可靠性的概率度量。工程结构可靠性,是指在规定时间和条件下,工程结构具有的满足预期的安全性、适用性和耐久性等功能的能力。由于影响可靠性的各种因素存在着不定性,如荷载、材料性能等的变异,计算模型的不完善,制作质量的差异等,而且这些影响因素是随机的,因而工程结构完成预定功能的能力只能用概率度量。结构能够完成预定功能的概率,称为可靠概率;结构不能完成预定功能的概率,称为失效概率。
幕墙结构设计的可靠性与建筑结构设计的可靠性要求是完全吻合的,幕墙结构体系的设计和选择与可靠性有着直接的关系。
2.2 机械可靠性
机械可靠性指产品在规定条件下和规定时间内完成规定功能的能力。包含4个要素(1)产品:任何设备(词条“设备”由行业大百科提供)、系统或元器件。(2)规定条件:包括使用时的环境条件和工作条件。环境条件:温度、湿度、振动、冲击、辐射等;工作条件:维护方法、储存条件、操作人员水平等。(3)规定时间:产品的规定寿命。(4)规定功能:产品必须具备的功能和技术指标。
固有可靠性指的是产品在设计、生产中已经确定的可靠性,它是产品内在的可靠性。与产品的制造、设计与生产有关;使用可靠性是指产品在使用中的可靠性,它与产品的运输、储藏、保管及使用过程中的操作水平、维修和环境等因素有关。
可见,机械系统和产品的可靠性与幕墙的产品可靠性要求也是一致的,幕墙产品种类也有很多,如铰链、风撑、预埋件、通风器等,而幕墙材料如玻璃、铝合金型材、结构密封胶等,也符合机械产品可靠性的概念。
2.3 建筑幕墙可靠性
工程结构的随机可靠性分析与机械系统和产品的可靠性分析从本质上均是基于经典可靠性理论。然而,工程结构的随机可靠性与机械产品等可靠性在一些重要方面还是有一定差别,因为机械产品多数是批量生产,且可以假定在名义上是相同的,可以根据统计概率得出破坏概率,但对工程结构尤其是大型工程结构常常无法以类似方法确定破坏概率。工程中需要预测结构破坏事件的数量,在设计阶段要从各个方面预估结构件强度或挠度特性,综合其概率模型。这个模型应该包括对所受载荷和结构抗破坏能力有影响的所有随机不确定因素。
从工程交付上看,幕墙是一个产品,具有机械可靠性的属性,可理解为可靠性是指建筑在满足建筑外观要求和幕墙设计使用年限内持续满足建筑幕墙物理性能的能力。从结构工程上看,幕墙可靠性是指在建筑幕墙使用年限内和各种自然作用下,幕墙结构具有满足预期的安全性、适用性和耐久性等功能的能力。由此可以看出,幕墙兼顾产品和结构功能的双重属性本质上是一致的,对幕墙产品可靠性定义可理解为:建筑幕墙的可靠性是指幕墙面板和支撑结构体系在设计使用年限内和正常设计、施工、使用条件下,达到预期的安全性、适用性和耐久性等建筑物理性能的能力。在这里,面板不仅是指玻璃、石材等面材,也包括板块之间嵌缝的密封胶、密封条;而支撑结构不仅包括受力龙骨、转接件(词条“转接件”由行业大百科提供)、埋件,也包括开窗器、铰链等有结构传力作用的五金附件。
2.4 结构可靠度
结构可靠度是结构可靠性的概率量度,即结构在规定的条件下和规定的时间内,完成规定功能的概率,是时间的概率。规定时间是指幕墙设计使用年限,目前国家和行业规范界定幕墙设计使用年限为25年;规定条件是指正常的设计、施工、使用条件,而不考虑认为过失所造成的事故。幕墙结构可靠度应该是结构安全性、适用性和耐久性的统称。
可靠度含有五个要素:对象、规定条件、规定时间、规定功能和概率。其中,前三个要素是可靠性的前提,是确切的具体的,这三个要素中不会也不允许包含模糊性,幕墙工程实践中的模糊性主要出现在对是否“完成规定功能”的判断和界定上,也就是说,在“完成”和“未完成”之间并不存在明显的界限,因此事实上,更准确的说法应该是“在某种程度上完成规定功能”,这样一来,可靠性的定义中就体现出了其可能存在的模糊性。因此,为了解决这个问题,引入了概率论和数理统计的数学模型,两者把实际问题中涉及到的模糊因素用数学表达式表示出来,使问题得以量化和精确化,可以将数学的研究对象从必然现象扩展到随机现象的领域,为人们比较准确地描述和处理具有模糊性的现象和事物提供了一种有效的数学手段。
根据工程结构设计的原理,幕墙结构可靠性的因素归纳为两个综合值,结构构件的荷载作用S和抗力(词条“抗力”由行业大百科提供)R,引入结构极限状态方程:
其中Z为结构功能函数。由于影响荷载作用S和结构抗力R分别有由很多其下属的基本随机变量(如形状、材性等)组成,将这些随机变量设为X1,X2,…,Xn ,则结构功能函数的一般形式为:

极限状态作为结构可靠性的临界判断状态,可分为承载能力与正常使用状态,其中承载能力极限状态对应于幕墙结构或构件达到最大承载能力或不适于继续承载的变形:
(1) 整个幕墙结构体系或其中一部分作为刚体失去平衡(如倾覆等);
(2) 幕墙结构构件或连续因材料强度被超过而破坏(包括疲劳破坏),或因过度的塑性变形而不适于继续承载;
(3) 幕墙结构转变为机动体系;
(4) 幕墙结构或结构构件丧失稳定(如压屈等)。
正常使用极限状态,对应于结构或结构构件达到正常使用或耐久性能的某项规定限值。
(1) 影响幕墙正常使用或外观的变形;
(2) 影响幕墙耐久性能的局部损坏(包括材料裂缝);由此可得出:
(a) Z > 0 结构可靠
(b) Z < 0 结构失效
(c) Z = 0 结构处于极限状态
以上是结构可靠性设计的基本判定公式。
引入可靠概率:结构能完成预定功能的概率(ps);失效概率:结构不能完成预定功能的概率(pf)概念:
失效概率pf 越小,结构的可靠性越高;失效概率pf 越大,结构的可靠性越低。通常以失效概率pf来度量结构可靠度。

图2.1安全概率和失效概率的关系图
实际上,失效概率pf的计算相当复杂,引用结构可靠指标β来代替失效概率pf,
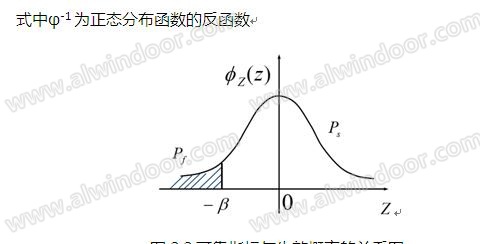
图2.2可靠指标与失效概率的关系图
如前面所述,当结构功能函数Z为多个随机变量组成的非线性函数时,且变量并不都服从正态分布或对数正态分布,此时基本上无法求解功能函数值,需要近似简化,以近似概率法分析可靠度,常见的有中心点法和验算点法,本文不在详述。
3 幕墙可靠性数学基础
3.1 可靠性分析中常用的概率分布
产品的可靠度都是随机变量,要运用概率论理论和方法来研究这些随机变量的规律。通常的做法是先讨论几种典型的已被证实的重要分布类型,再把产品的现场或试验数据用计算机进行模拟,进行统计学处理,用来判别处理结果和哪一种分布函数吻合,则称这种随机变量符合某种函数分布,运用函数分布曲线,可快速简便估算出某一时刻的函数值,即可靠度。与幕墙工程相关的常见的分布函数有:二项分布、泊松分布、正态分布、对数正态分布、指数分布、威尔分布等。
(1) 离散型随机变量的分布:随机变量可能的取值为有限个,每一个不同的变量值对应一个明确的概率值。

(2) 连续性随机变量:在给定区间(或无限区间)内可取的任意数值的随机变量。通常电子零部件、机械产品的寿命都属于连续性随机变量,如幕墙开启扇执手、铰链、电动开窗器(词条“电动开窗器”由行业大百科提供)等,


计算结果如下表3-1:
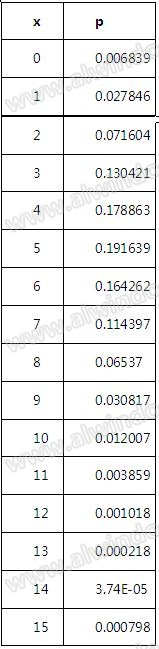
绘制图形为图3-1:
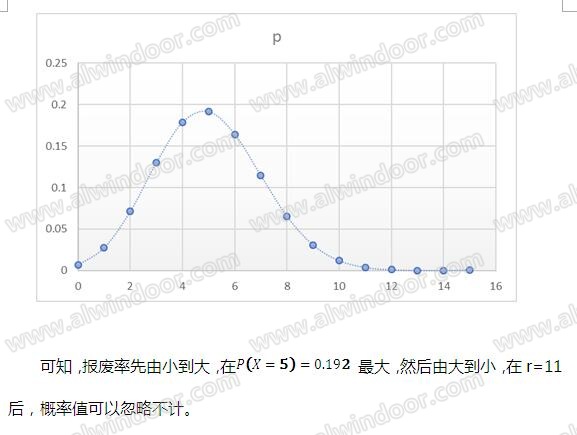





4 小结
本文针对工程可靠性概念,对幕墙结构可靠性的原理概念进行了梳理和定义,兼具结构工程和机械产品的双重功能的幕墙系统,具有复杂的功能,文章介绍了用于可靠性研究的基本数学模型,并对幕墙部分产品可靠度计算举例,阐明了以后可靠性分析所用的基本数学工具。
由于篇幅有限,后续相关针对幕墙可靠性设计与分析的方法、案例应用的论述,另文详叙,待续未完。
参考文献
[1]国家标准《建筑幕墙》,GB/T21086-2007
[2]国家标准《建筑可靠度统一设计标准》,GB 50068-2001

